Palindromické číslo je „symetrické“ číslo, jehož hodnota se nezmění, pokud jeho číslice napíšeme v opačném pořadí. Příkladem jsou tedy čísla 2, 55, 121, 1991, 12345678987654321.

Pokud vezmeme libovolné přirozené číslo a přičteme k němu jeho zrcadlový obraz (stejné číslo napsané v opačném pořadí) a tuto operaci  budeme stále opakovat, získáme velmi často po konečném počtu opakování palindromické číslo.

Jedná se o velmi jednoduchý proces:

1. Nechť x je libovolné přirozené číslo a y je jeho zrcadlový obraz
2. Provede se operace x+y
3. Pokud součet netvoří palindrom, přejde se zpět k druhému kroku

Například:

123 + 321 = 444

nebo

78 + 87 = 165, 165 + 561 = 726, 726 + 627 = 1353, 1353 + 3531 = 4884.

Existují však čísla, u nichž se neví, zda se po konečném počtu opakování algoritmu lze k palindromickému číslu dostat. Takovým číslům říkáme kandidáti na Lychrelovo čísla. Lychrelovo číslo (anglicky Lychrel number) je tedy přirozené číslo, které nemůže vytvořit palindromické číslo opakováním procesu sčítání původního čísla s jeho zrcadlovým obrazem. Některá čísla vytvoří palindrom po několika opakováních (iteracích) tohoto procesu, přesněji 80% přirozených čísel do 10 000 vytvoří palindrom po čtyřech nebo méně krocích a 90% vytvoří palindrom do sedmi kroků. Ale například číslo 89 vytvoří palindrom (8 813 200 023 188) až po 24 krocích. Nejmenším kandidátem na Lychrelovo číslo je tedy 196, dále pak následují 295, 394, 493, 592, 689, 691, 790, 879… Různá čísla mají tedy různý počet iterací, který je potřebný k vytvoření palindromu.
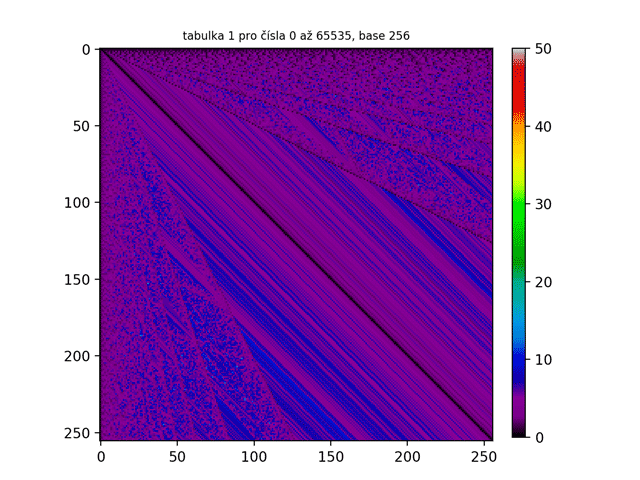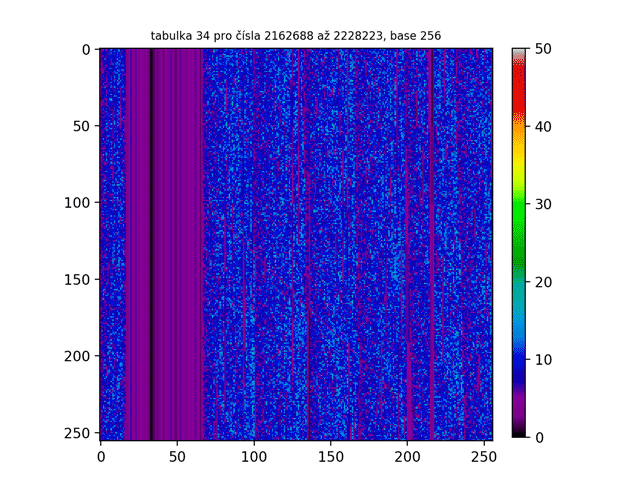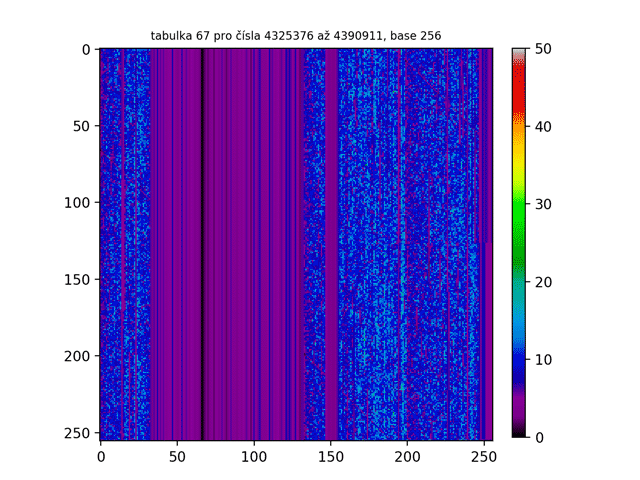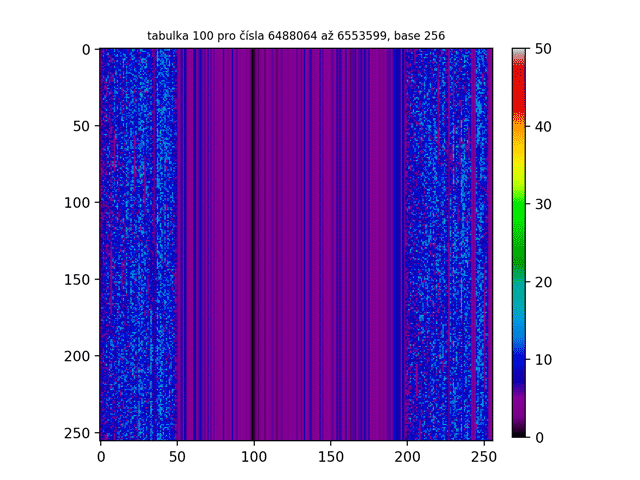
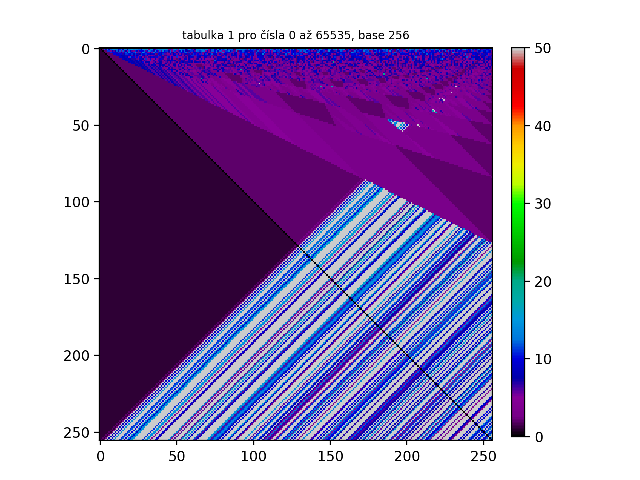
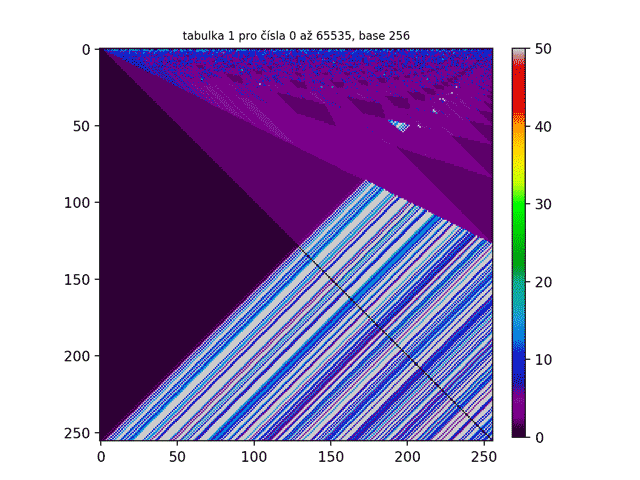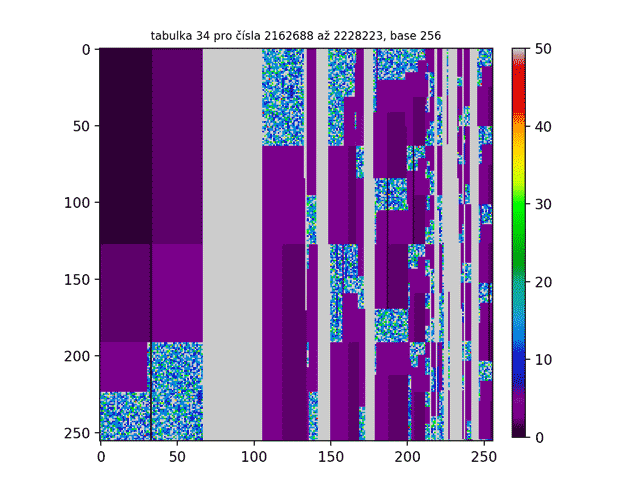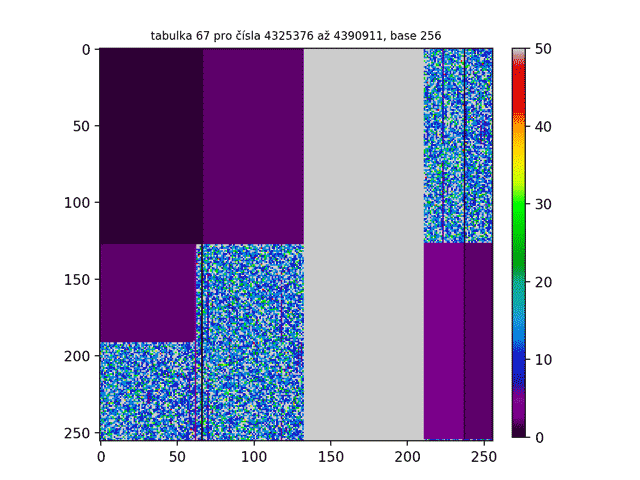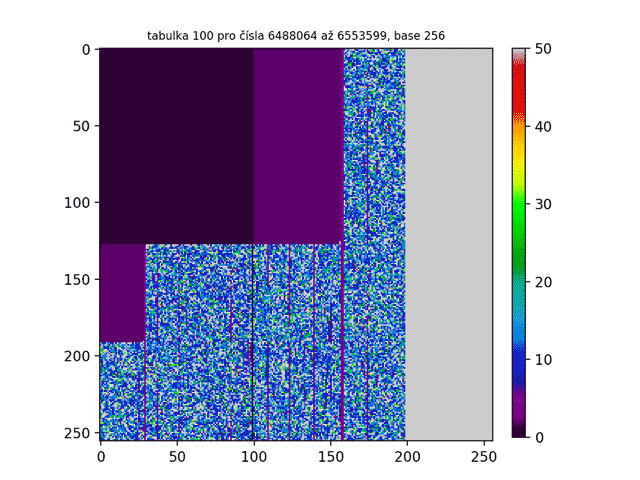
Pro vizualizaci počtu kroků potřebných k vytvoření palindromu z určitých čísel jsem vytvořil čtvercovou tabulku a do ní vepsal celá čísla v rozsahu 0-99. Tuto tabulku lze matematicky chápat jako 10x10 matici. Podle toho, kolik kroků bylo potřeba k vytvoření palindromu z čísla v určitém políčku tabulky jsem políčko vybarvil dle přiřazených barev (viz spektrum vpravo vedle tabulky) a vytvořil tak výsledný obrazec.

V tomto procesu jsem se rozhodl pokračovat, a proto jsem vytvořil navazující tabulky v číselném rozsahu 100-199, 200-299, 300-399... 

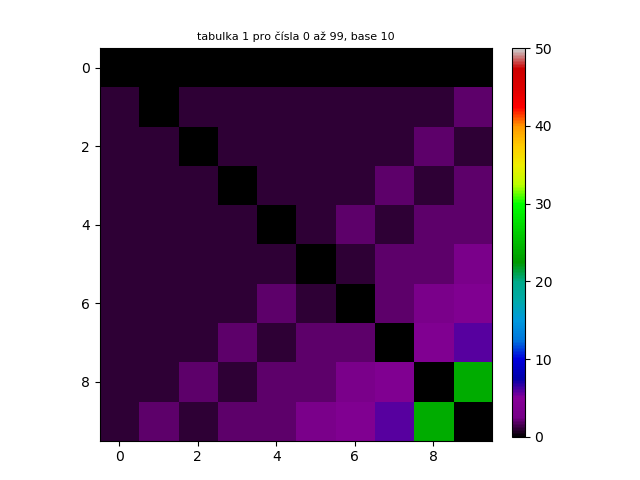
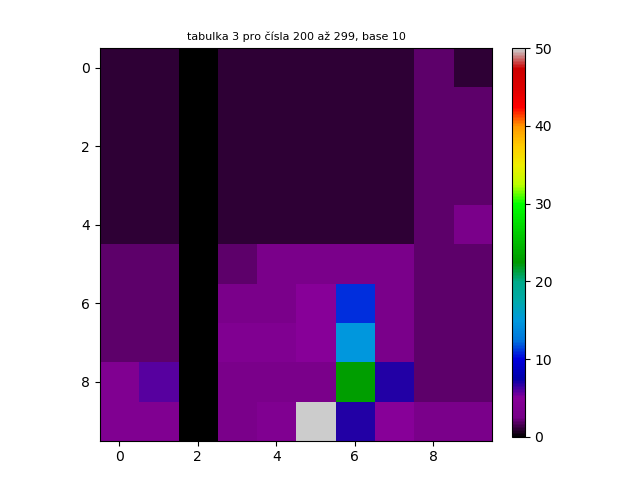
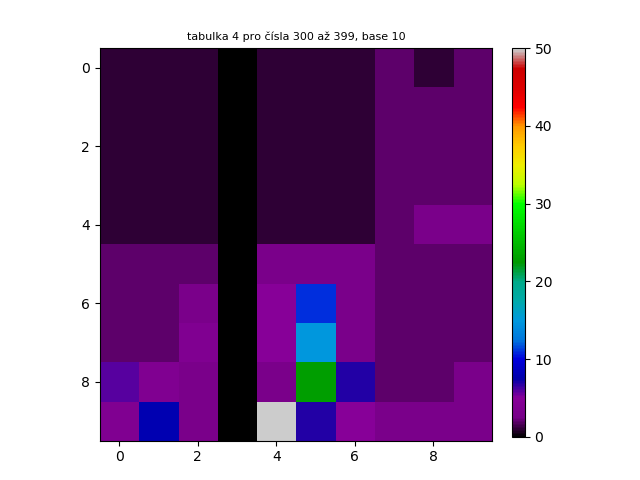
Těchto tabulek je možné generovat nekonečně mnoho. Pro náhled jsem prvních 300 tabulek chronologicky seřadil a udělal z nich animovaný GIF. Jak lze vidět, tabulky na sebe navazují podobně jako skutečná animace.

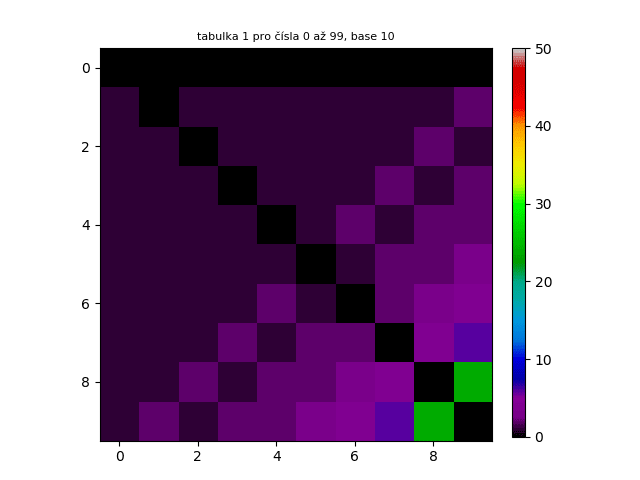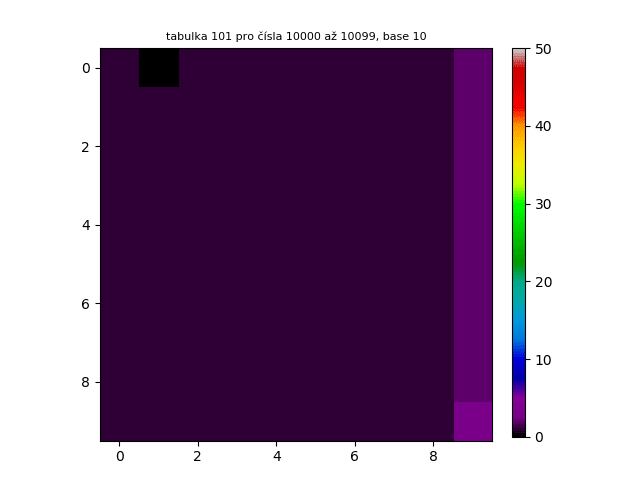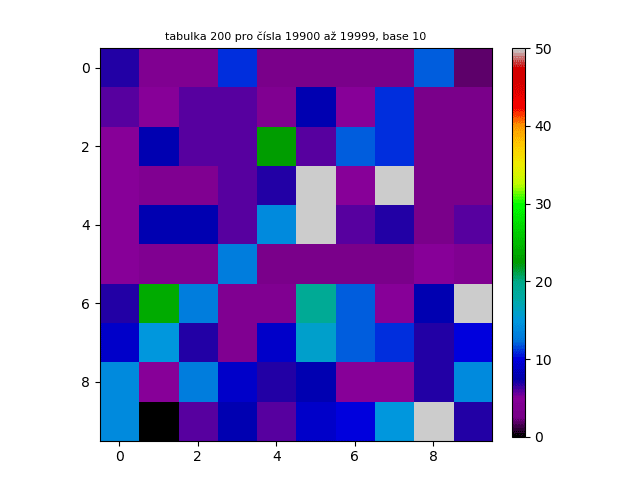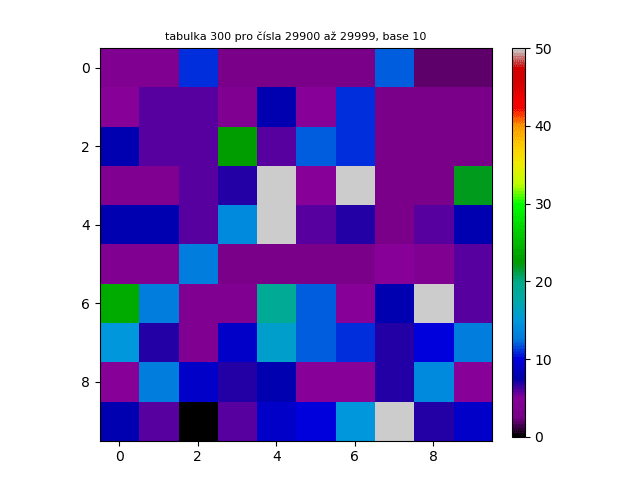
Je velice důležité zmínit, že ještě nikdo matematicky nedokázal, že kandidáti na Lychrelovo čísla jsou skutečně Lychrelovo čísla. Jinými slovy - nikdo neví, zda např. z čísla 196 přeci jenom po mnoho krocích nevznikne palindrom. V roce 2012 se Jason Doucette, Wade VanLandingham a Romain Dolbeau pokusili z tohoto čísla vytvořit palindrom. Zkusili přes bilión kroků, ovšem palindrom nenalezli. To ovšem není důkaz pro to, že z tohoto čísla nelze vytvořit palindrom. Možná vznikne až po bilión prvním kroku. Jisté je jedno - pokud z tohoto čísla nelze vytvořit palindrom, tato metoda hrubé síly nám nikdy nezodpoví tuto otázku.

Protože pro generování těchto obrazců jsem vytvořil program v jazyce Python, z praktického hlediska jsem musel nastavit něco jako „brzdu“ (v mém programu je nastavena na 50 kroků), která stanoví maximální počet kroků. Proto je tedy číslo 50 maximální hodnota spektra vpravo od tabulek. Pokud by totiž taková brzda neexistovala, program by se zasekl při nekonečných pokusech o vytvoření palindromu z čísel, ze kterých ani nejspíš palindrom vytvořit nelze.

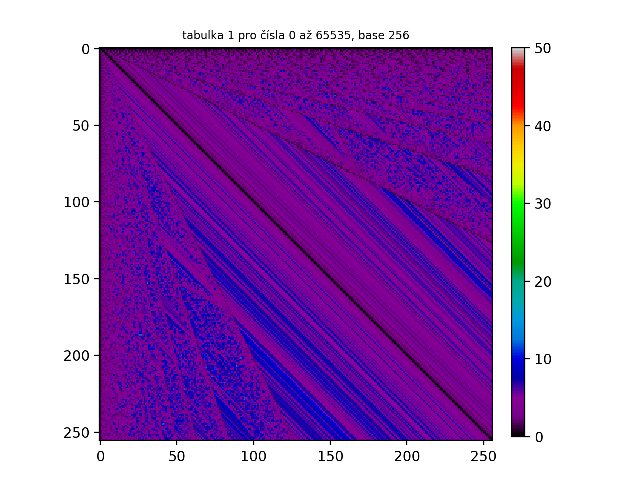
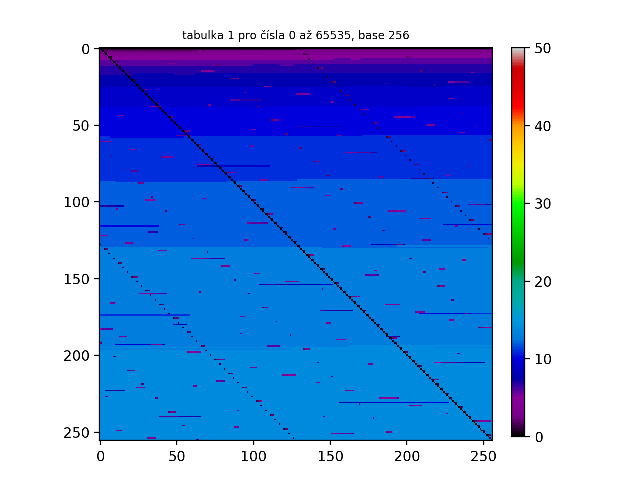
Důležité je uvědomit si, že tyto palindromy jsou vázány na naší desítkovou soustavu. Tak například číslo 255 v naší desítkové soustavě rozhodně palindrom není, ovšem v hexadecimální soustavě bychom toto číslo zapsali jako FF - a to už palindrom je! Těmto rozdílným číselným soustavám se také říká base. Desítkovou soustavu tak můžeme nazvat base 10, hexadecimální soustavu base 16, binární soustavu base 2 atd. Nabízí se tedy otázka: Jak by vypadaly tabulky v jiných base? Vzhledem k tomu, že naše originální tabulka pro base 10 měla rozměry 10x10 políček, tabulky pro vyšší base (řekněme base N) budou mít rozměry NxN políček. Jak lze vidět na animovaném GIFu pro tabulku 1 níže, čím větší je base, tím „ostřejší“ je obrazec. 

Až nyní se nám tato struktura ukázala v plné své kráse a jak lze vidět, struktura tabulky 1 je ve všech base stejná. A co jiné tabulky? Je struktura tabulky 2 také ve všech base stejná? Jak lze vidět na GIFu níže, odpověď je kladná.

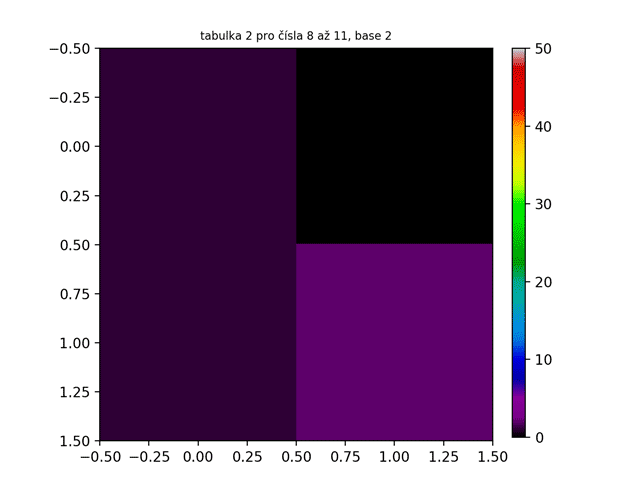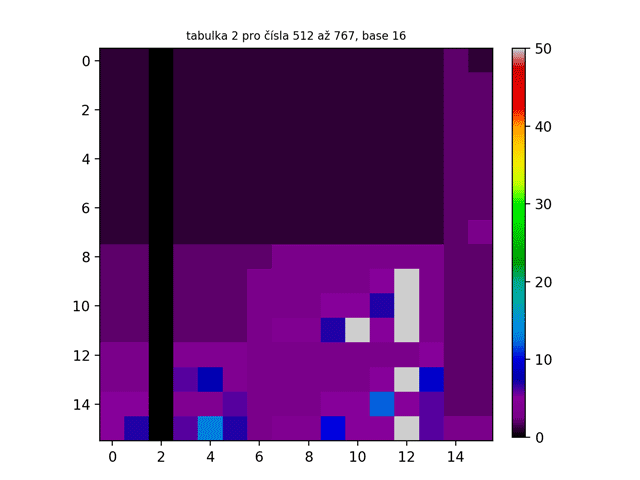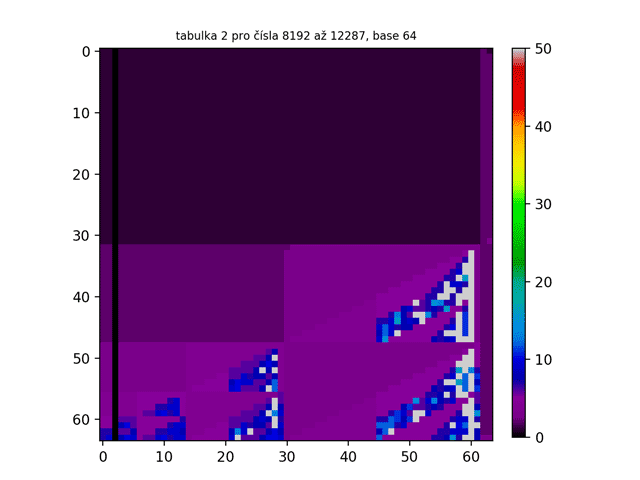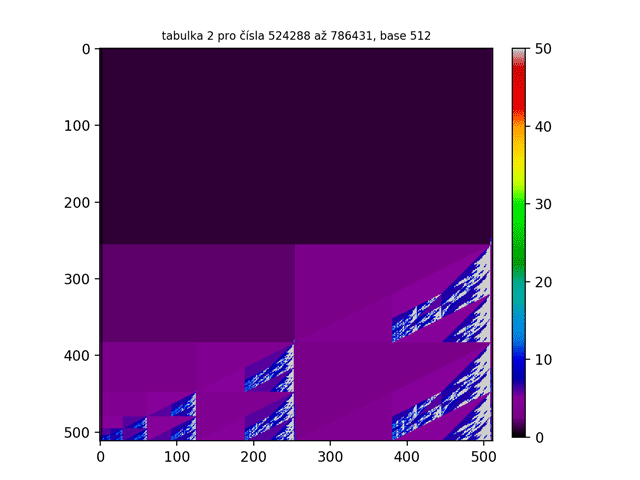
Na tabulce 2 lze nyní spatřit náznaky rekurze. Neměly bychom se tomu ani příliš divit - vždyť obrazec přece vznikl rekurzivním procesem. Dalo by se říci, že jsme právě vytvořili fraktál, protože tabulka 2 splňuje všechny podmínky pro to, aby nějaký objekt byl nazván fraktálem: 

1. Je soběpodobný – znamená to, že pokud daný útvar pozorujeme v jakémkoliv měřítku či rozlišení, pozorujeme stále opakující se určitý charakteristický tvar (motiv);
2. Mívá na první pohled velmi složitý tvar, ale je generován opakovaným použitím jednoduchých pravidel.

Na prvním GIFu jsme již viděli prvních 300 tabulek. To nám odhalilo ovšem pouze špičku ledovce! Jak tedy třeba vypadá miliontá tabulka ve vyšších base? Nebo bilióntá tabulka? A jak bude vypadat, když budu tabulkami chrologicky listovat a vytvořím z nich animaci jako tomu bylo v prvním GIFu? Níže jsou obrázky takových „vyšších“ tabulek. Jak z nich lze  zpozorovat, čím vyšší je pořadí tabulky, tím více je Lychrelovo čísel tabulka obsahuje (a proto jsou obrazce bělejší).

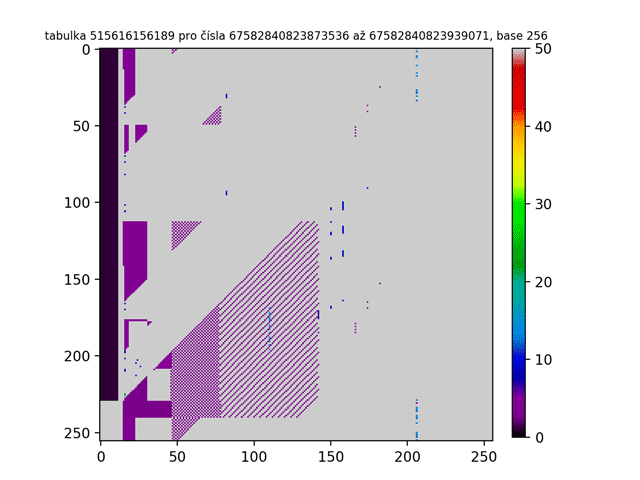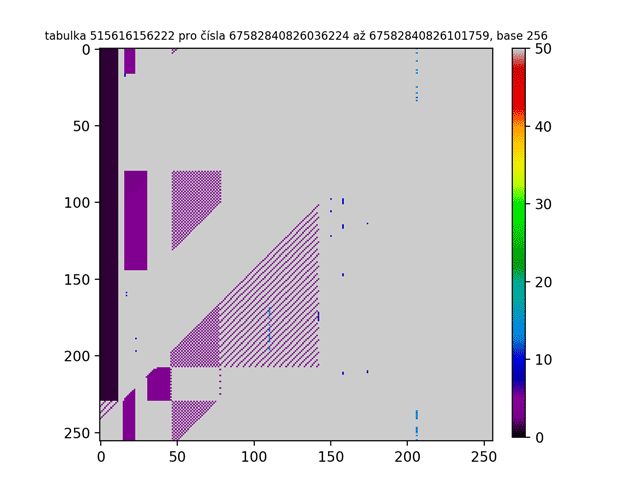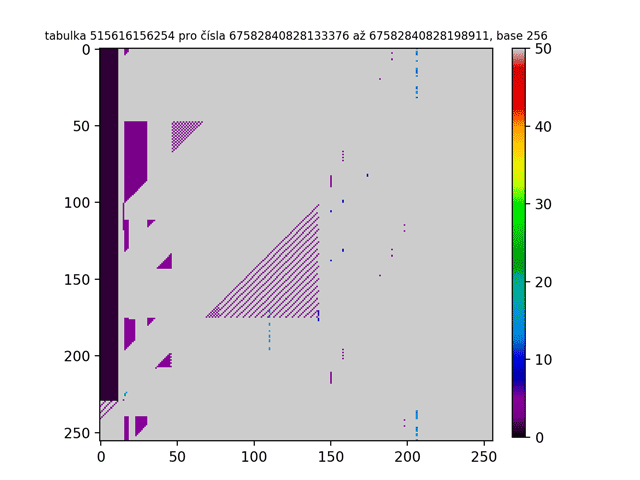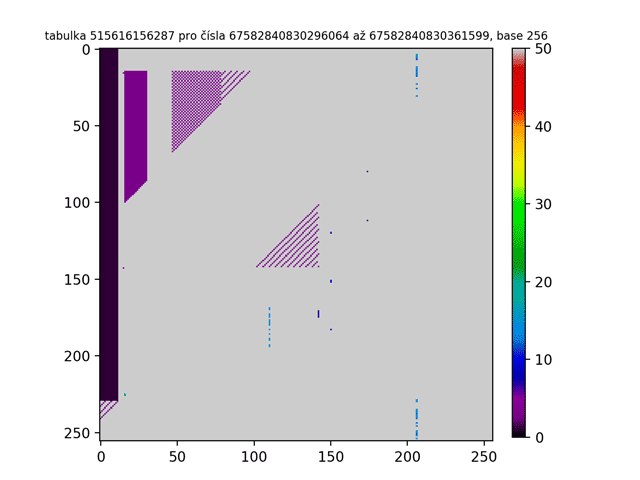
Tímto jsme odhalili tuto strukturu natolik, že nevím, jak dále pokrčovat. Ještě tu ovšem vidím jednu možnost experimentace. Na začátku tohoto článku jsou uvedeny jednotlivé kroky, které jsou slouží jako návod pro to, jak se dostat (nebo nedostat) k palindromu. Pro zajímavost si dovolím tyto kroky poupravit a definovat tak nový proces:

1. Nechť x je libovolné přirozené číslo a y je jeho zrcadlový obraz
2. Proveďe se operace (x+y) mod x
3. Pokud výsledné číslo netvoří palindrom, přejde se zpět k druhému kroku

Když vytvoříme díky těmto novým pravidlům tabulky, jakož jsme to učinili předtím a budeme jimi listovat, vytvoří se tato animace:

Výsledek je to vskutku pozoruhodný. A jak je zřejmé, variací pravidel je nekonečně mnoho. Zde je tedy ještě několik příkladů takovýchto pozměněných pravidel a pod nimi se vždy nacházejí příslušné vizualizace:

1. Nechť x je libovolné přirozené číslo a y je jeho zrcadlový obraz
2. Provede se operace (x+y) mod x+x
3. Pokud výsledné číslo netvoří palindrom, přejde se zpět k druhému kroku

1. Nechť x je libovolné přirozené číslo
2. Provede se operace (2*x) : 3
3. Výsledek druhého kroku se zaokrouhlí nahoru
4. Pokud výsledné číslo netvoří palindrom, přejde se zpět k druhému kroku

Pokud by měl někdo zájem experimentovat s programem pro generování těchto obrazců, zde je zdrojový kód v jazyce Python, který jsem vytvořil: