V této práci jsem se zabýval odrazem, jeho vizualizací a matematickým modelem. Začal jsem jednoduchým problémem – míčkem ve čtverci. Tento „míček“ je ve skutečnosti matematický vektor, tedy bezrozměrný bod, který má pozici a směr, ale pro zjednodušení ho budeme nadále nazývat míčkem. Také jsem pro zjednodušení ignoroval odpor vzduchu, ztrátu energie při odrazu atd. Míček je tedy vržen do čtverce pod nějakou počáteční pozicí a úhlem. Když narazí na stranu čtverce, odrazí se. Při pohybu za sebou také zanechává trajektorii. Tuto simulaci lze vidět v interaktivním okně níže. Lze s ním experimentovat a měnit počáteční úhel (angle) na jinou hodnotu. Dále stačí jen zmáčknout tlačítko Run (popřípadě Stop a poté znovu Run, pokud program již běží) a kód se spustí. Jak lze vidět, počáteční úhel ovlivňuje celkový vzhled trajektorie. Stejným způsobem lze zvýšit i rychlost (speed). Dokonce lze přidat překážku tím, že se přepíše is_obstacle = False na is_obstacle = True.

Zatímco některé hodnoty počátečního úhlu vytvoří velice jednoduché trajektorie, které samy sebe obtahují (při úhlech 45° a 90°), jiné hodnoty vytvoří velmi chaotické trajektorie. Otázka je, zda se jednou po dostatečném počtu odrazů i tyto trajektorie uzavřou samy do sebe a začnou se jen obtahovat. Jak lze spatřit na nákresu níže, každému odrazu lze přiřadit nějaký úhel φ(n) a nějakou délku L(n) od levého kraje strany čtverce, na níž míček dopadl.

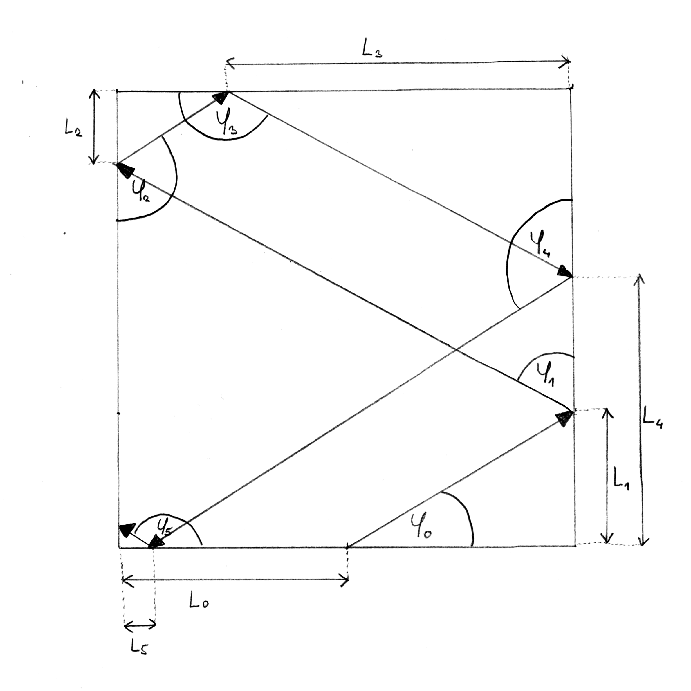
Každá strana je velká 1 jednotku. Počátečními parametry je tedy velikost úhlu φ(0) a délka od levého kraje strany L(0). Takto vypuštěný míček se pak odrazí a vzniknou dvojice čísel φ(1) a L(1), dále φ(2) a L(2) atd… Pokud tedy chceme dokázat, zda se trajektorie při určitém počátečním úhlu a délce od levého kraje strany uzavře, zajímá nás, zda existují čísla φ(n) a L(n) taková, že φ(0) = φ(n) a L(0) = L(n). Jinými slovy, zajímá nás, zda se míček jednou dostane na místo, odkud byl vypuštěn a od toho se odrazí pod stejným úhlem. Abychom přesněji pochopili, co se z matematického hlediska při odrazech děje, napsal jsem algoritmus, do kterého se zadají dva parametry – φ(n) a L(n). Algoritmus poté přesně vypočte hodnoty čísel φ(n + 1) a L(n + 1), tedy hodnoty dalšího odrazu.

POKUD φ(n) < 90°:

            POKUD tan(φ(n)) * (1 – L(n)) < 1:

                        φ(n + 1) = 90° - φ(n)

                        L(n + 1) = tan(φ(n)) * (1 – L(n))

            POKUD tan(φ(n)) * (1 – L(n)) = 1:

                        φ(n + 1) = φ(n)

                        L(n + 1) = 0

            POKUD tan(φ(n)) * (1 – L(n)) > 1:

                        φ(n + 1) = 180° -  φ(n)

                        L(n + 1) = 1 – (tan(90° - φ(n)) + L(n))

POKUD φ(n) = 90°:

            φ(n + 1) = φ(n)

            L(n + 1) = L(n)

POKUD φ(n) > 90°:

            POKUD tan(180° -  φ(n)) * L(n) < 1:

                        φ(n + 1) = 270° - φ(n)

                        L(n + 1) = 1 – (tan(180° - φ(n)) * L(n))

            POKUD tan(180° -  φ(n)) * L(n) = 1:

                        φ(n + 1) = φ(n)

                       L(n + 1) = 1

            POKUD tan(180° -  φ(n)) * L(n) > 1:

                        φ(n + 1) = 180° - φ(n)

                        L(n + 1) = 1 + tan(150° - φ(n)) - L(n)

Stačí nám tedy do algoritmu vložit použe dva základní parametry (výchozí úhel a pozici) a on nám dá dva parametry kroku následujícího. Tyto dvojice čísel můžeme postupně vkládat do množiny číselné posloupnosti (nazvěme tuto množinu M). Otázka "Uzavře se jednou trajektorie míčku?" je logicky ekvivalentní s otázkou "Je posloupnost M periodická?". Zatím bohužel nevím, jak na tuto otázku odpovědět. 

Rozhodl jsem se dále pracovat na simulaci odrazu a rozšířit ji do 3D. Míček se v ní odráží od stěn krychle v trojdimenzionálním prostoru. Bohužel tato simulace nelze použít na webu ve formě interaktivního rámečku. Proto je zde pouze kód a výstup v podobě obrázků.

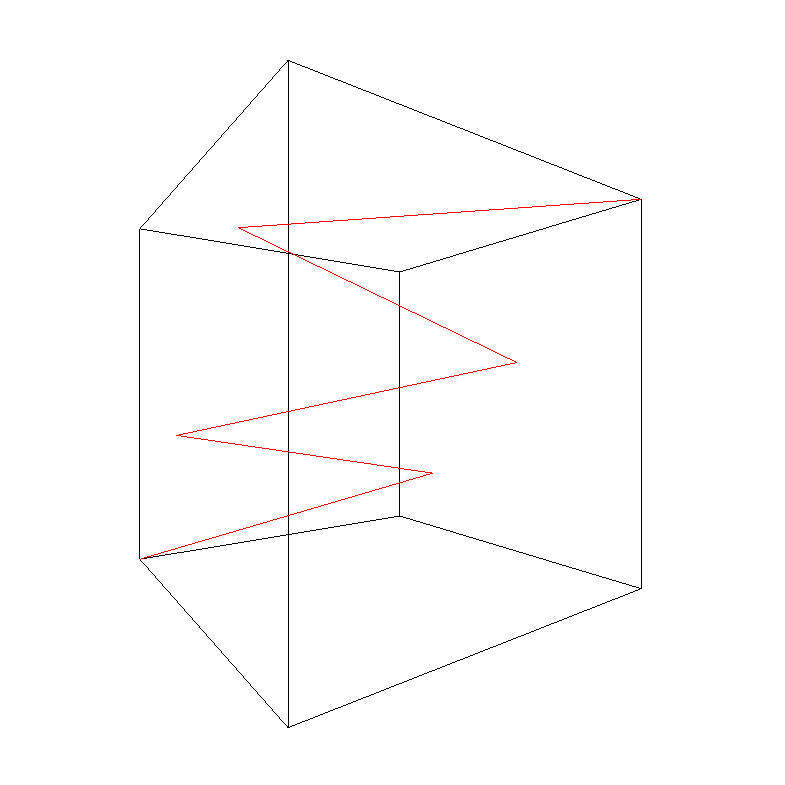
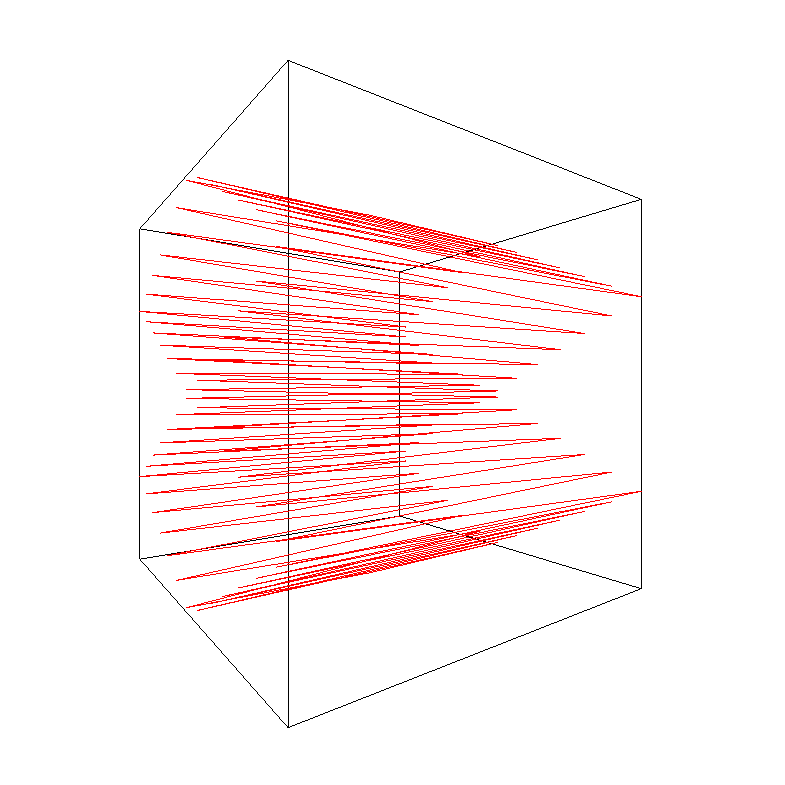
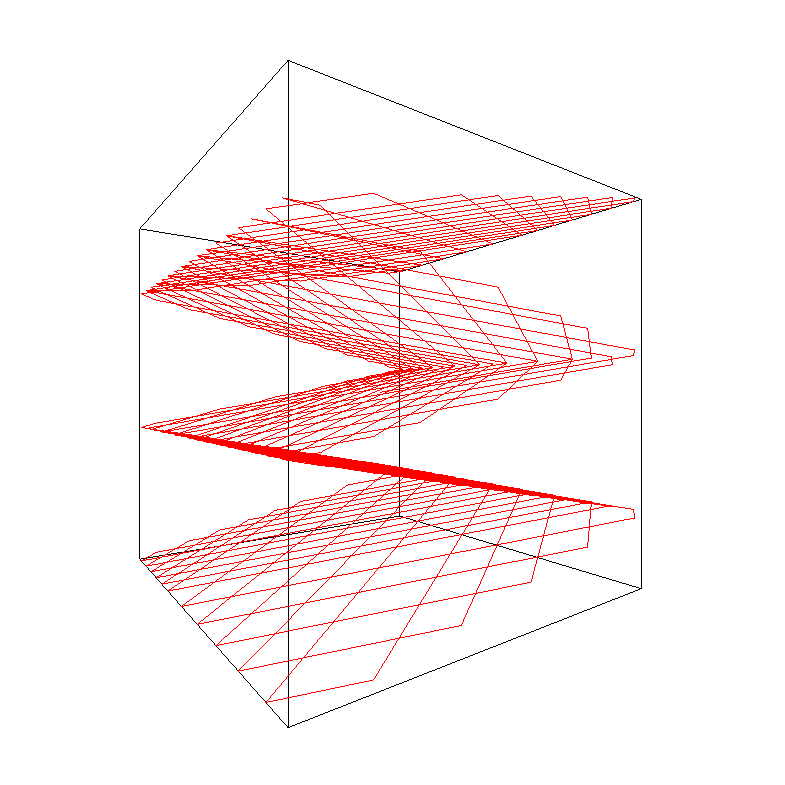
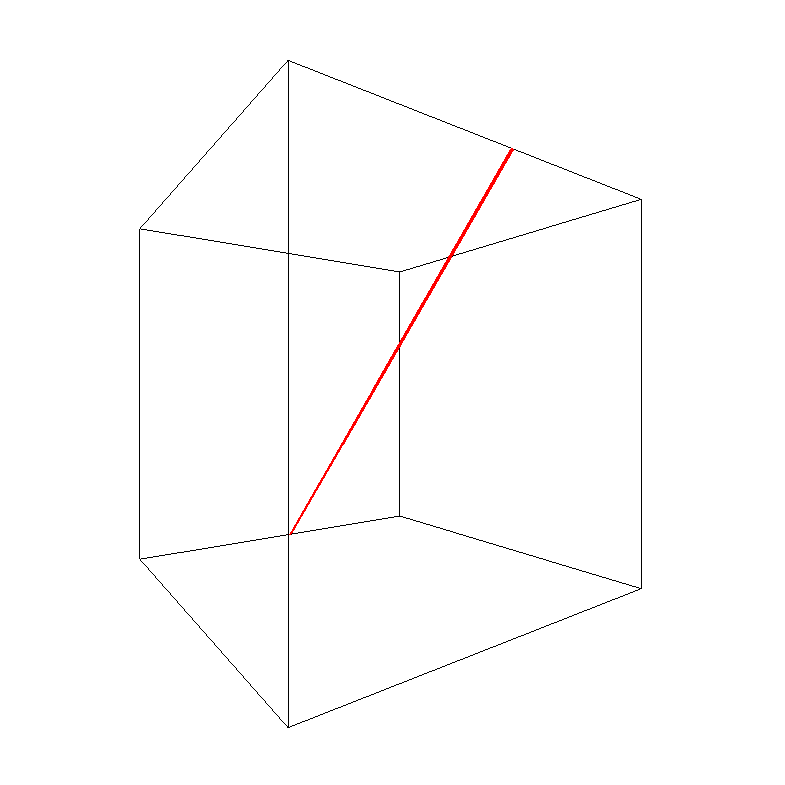
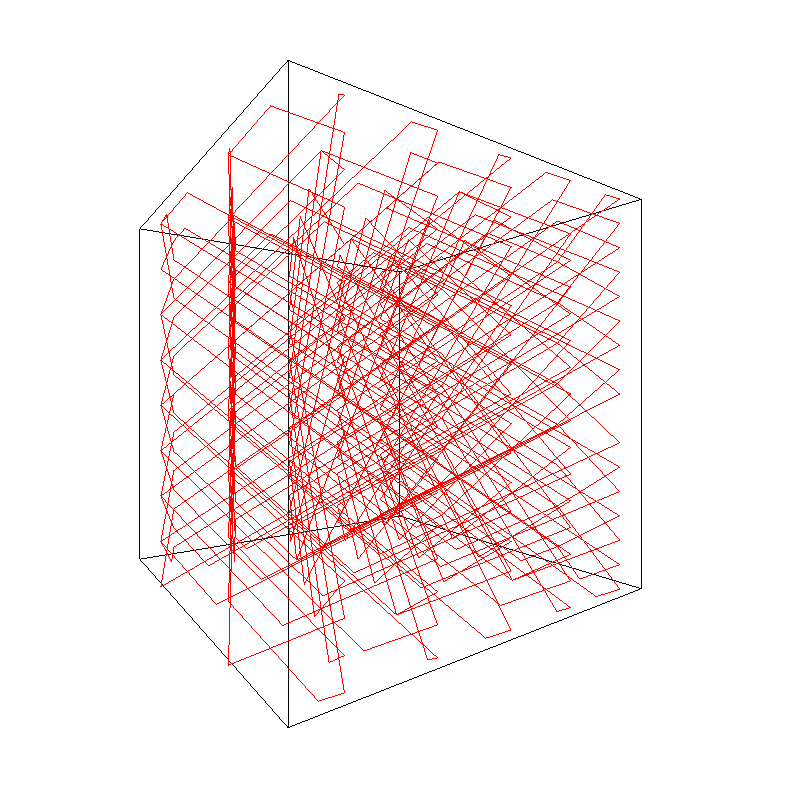
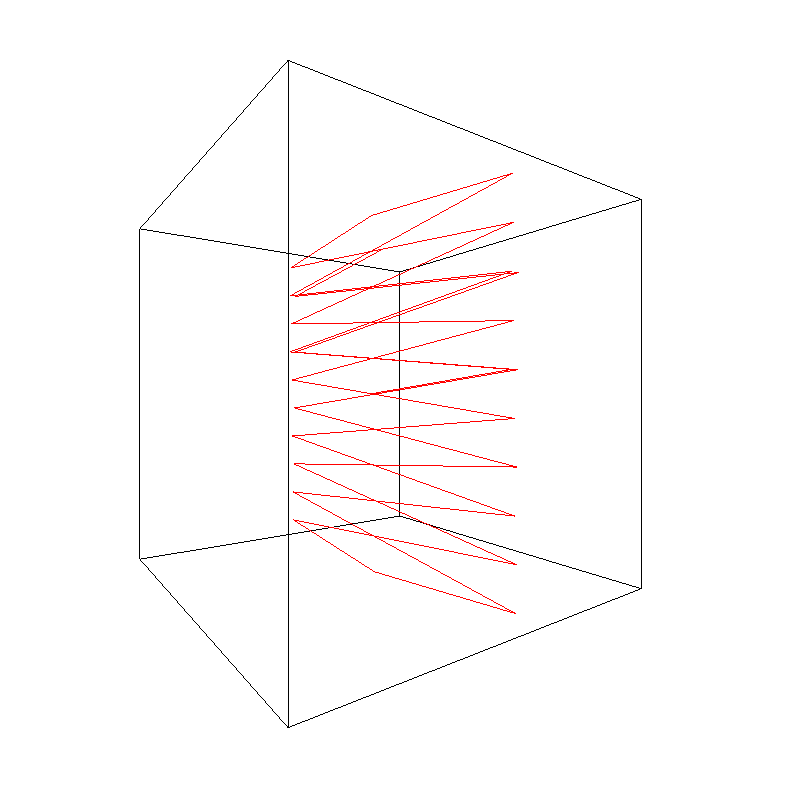
Různé obrázky výše jsou generovány vypuštěním míčku ze středu krychle do různých směrů. Jak lze vidět, tento počáteční směr zásadně ovlivňuje podobu trajektorie. Některé trajektorie se uzavřou samy do sebe hned po několika odrazech, jiné vypadají spíše chaoticky. Stejně jako u 2D simulace je dost obtížné určit, zda se náhodou i velice chaoticky vypadající trajektorie po dostatečném počtu odrazů uzavřou samy do sebe a dále se budou jen opisovat. Níže je kód, který jsem pro tuto 3D simulaci vytvořil.