Asi nejznámější věcí je v populární matematice Fibonacciho posloupnost. Je to dáno jednak svou elegantní jednoduchostí, ale také jejím uplatněním hned v několika nevědeckých oborech, jako jsou například hudba nebo umění. Někteří lidé jí přisuzují až magické schopnosti a tvrdí, že tato posloupnost „vládne vesmíru“ nebo, že je „otiskem prstu Boha“. Na internetu se o ní ale bohužel šíří mylné informace, kterými se zde budu zabývat. Všichni tuto posloupnost nejspíš známe, přesto jí v úvodu pro jistotu vysvětlím.

Fibonacciho posloupnost je definovaná vzorcem

F(0) = 0, F(1) = 1,

F(n) = F(n - 1) + F(n - 2).

Tento vzorec jde jednoduše slovně vysvětlit. První dva členy této sekvence jsou čísla 0 a 1 (proto F(0) = 0 a F(1) = 1). Následně tyto dva členy sečteme (tedy 1 + 0) a vznikne nám třetí člen posloupnosti, kterým bude číslo 1. Posloupnost tedy vypadá následovně: 0, 1, 1. Dále znovu sečteme poslední dva členy (tedy 1 + 1) a vznikne nám číslo 2. Vznikne posloupnost 0, 1, 1, 2. Znovu sečteme poslední dva členy (tedy 2 + 1) a výsledné číslo znovu přidáme do posloupnosti. Takto pokračujeme až do nekonečna. Prvních několik člen této posloupnosti vypadá takto:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Tato posloupnost má překrásné matematické vlastnosti. Tak například, pokud vezmeme dvě po sobě jdoucí čísla a vypočítáme jejich podíl F(n + 1) / F (n), vznikne nám aproximace matematické konstanty φ, tedy zlatého řezu. Například 144 / 89 = 1,6179775280898876404494382022472, což je velice blízko zlatému řezu. Čím vyšší čísla zvolíme, tím přesnější aproximace bude. Vzhledem k tomu, že φ je iracionální číslo (má nekonečný neperiodický desetinný rozvoj), tato aproximace nemůže být nikdy naprosto přesná.

Také pomocí této posloupnosti lze zkonstruovat velice slavnou spirálu zlatého řezu. Stačí jen vytvořit čtverec o rozměrech 1x1, poté další čtverec o rozměrech 1x1, následně další čtverec 2x2, 3x3, 5x5, 8x8… Poté už stačí jen do čtverců narýsovat čtvrtinu kruhu. Tento postup je dobře znázorněn v animaci níže.

Tady můžeme vidět hned první mýtus. Často na internetu vidím obrázky ulity loděnky, která má prý tvar Fibonacciho spirály. To je ale nesmysl a jak je hned z obrázků níže patrné, tato spirála absolutně neodpovídá tvaru ulity tohoto tvora. 

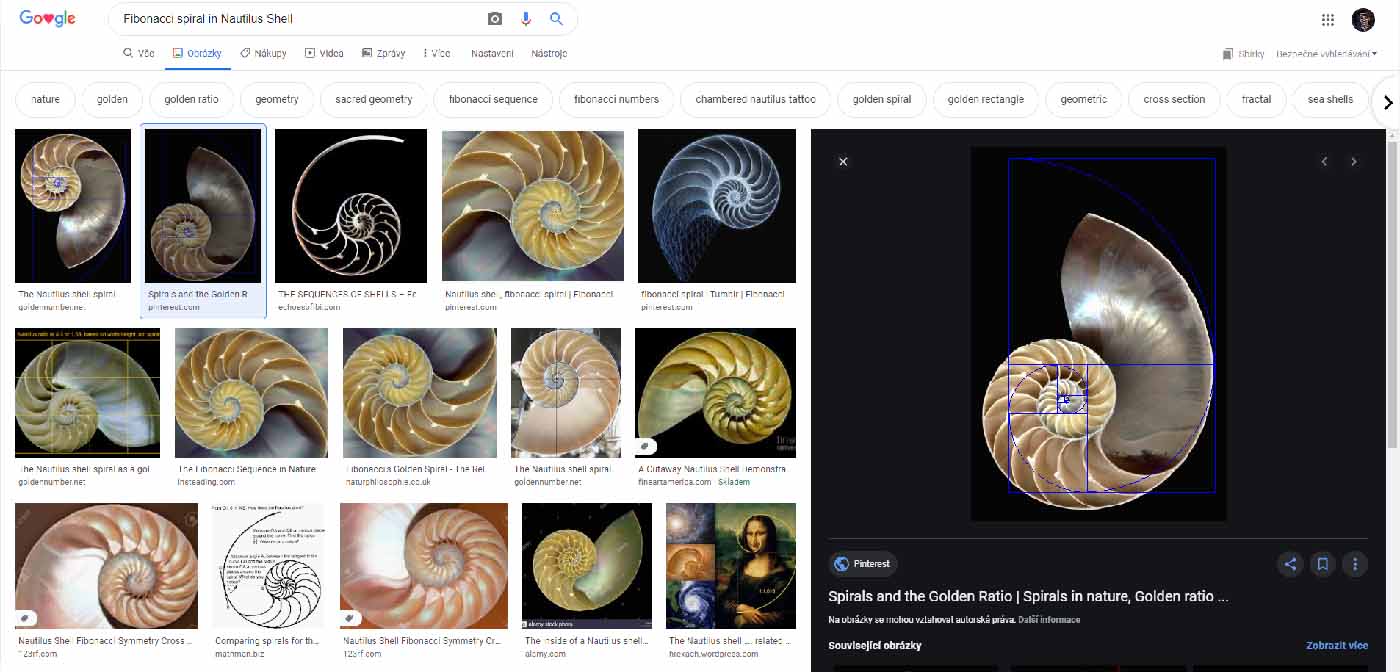
Zdroj: Google obrázky

Zdroj: youtube.com

Ve skutečnosti nemá loděnka ulitu ve tvaru Fibonacciho spirály (obrázek vlevo), ale logaritmické spirály (obrázek vpravo).

Dalším mýtem je tvrzení, že počet okvětních lístků rostlin je dán Fibonacciho posloupností. Zastánci tohoto mýtu tvrdí, že sice existují květiny, které mají počet okvětních listů jiný než členy Fibonacciho posloupnosti, ovšem takových je podle nich jen málo. Rozhodl jsem se toto tvrzení prověřit, a proto jsem si vzal atlas rostlin a spočítal téměř u každé rostliny počet okvětních lístků (některé květiny jsem vynechal proto, že mají například samčí i samičí květy s rozdílným počtem okvětních lístků nebo jim okvětní lístky úplně chybí). Z botanického hlediska je ovšem pojem „okvětní lístek“ dost nepřesný. To, čemu se hovorově říká okvětní lístek se v botanice nazývá květní obal. Ten se dále dělí na korunní lístek a kališní lístek (viz obrázek níže). Někdy jsou tyto dva listy srostlé a tvoří tak jeden takzvaný okvětní lístek.

Do excel tabulky jsem tedy vypsal ke jménům květin počet jejich korunní lístků a kališních lístků, nebo okvětních lístků. Ze 120 rostlin, která byly uvedeny v knize Kapesní ATLAS ROSTLIN od Alberta Piláta a Otto Ušáka jsem takto přepsal do excel tabulky 104 rostlin. Z těchto dat jsem poté pomocí programovacího jazyka Python vytvořil níže uvedený graf.

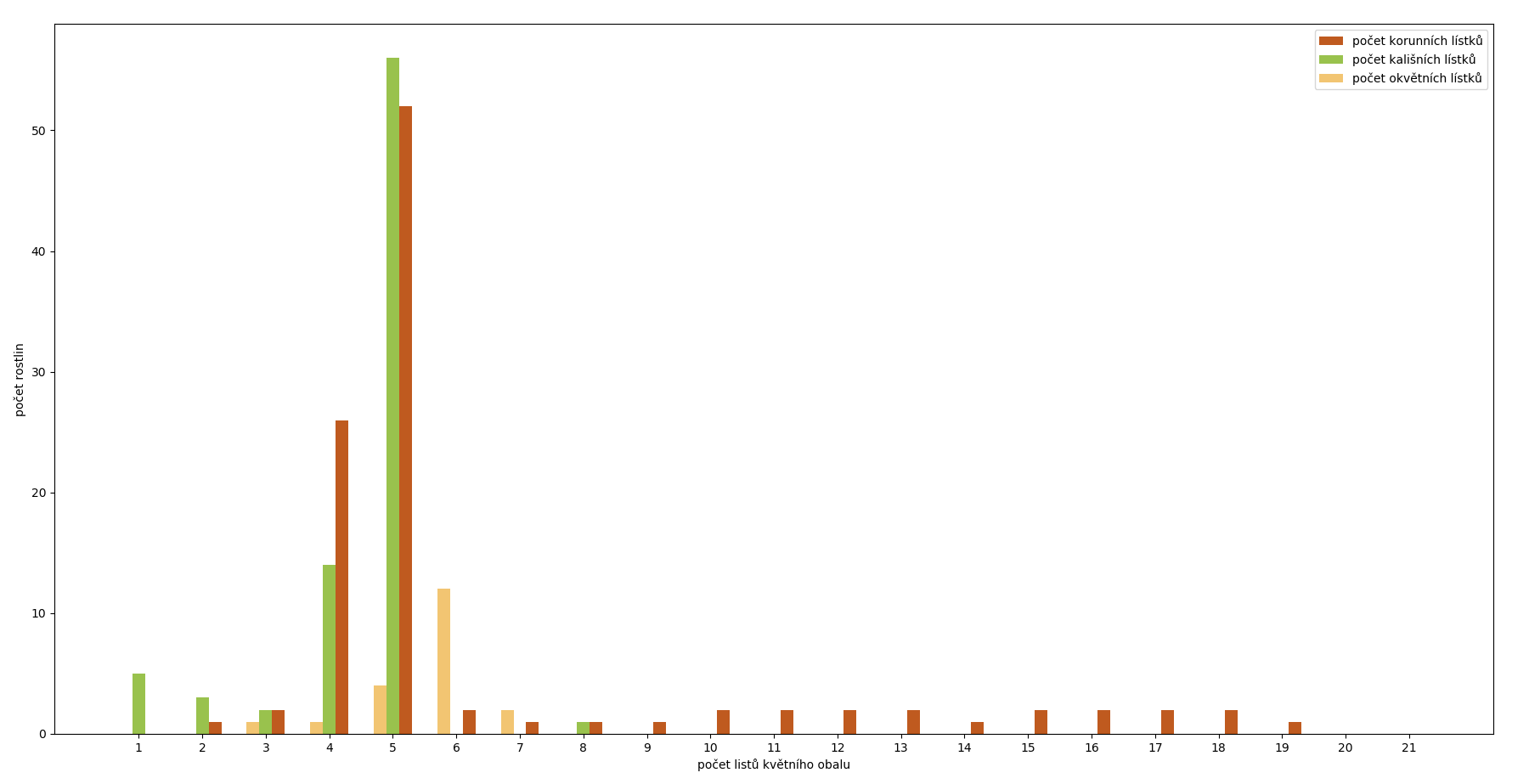
 Jak je z něho patrné, nejčastěji mají květiny 5 lístků květního obalu, což je zrovna náhodou číslo Fibonacciho posloupnosti. To je ale vše, jelikož druhým nejčastějším případem je číslo 4 a to není číslo Fibonacciho posloupnosti. Kdyby toto tvrzení bylo pravdivé, v grafu by to bylo patrné. Mýtus je tím tedy vymýcen, Fibonacciho posloupnost s počtem lístků květního obalu vůbec nesouvisí. 

Tyto dva mýty určitě nejsou jediné, ale mým úkolem nebylo vymýtit všechny, ale spíše poukázat na to, že některé věci, které lze najít na internetu o Fibonacciho posloupnosti a zlatém řezu jsou nesmysl a vždy je důležité se nad nimi nejdříve zamyslet. Tím samozřejmě nechci zpochybňovat celou Fibonacciho posloupnost, pravdou je, že má opravdu pozoruhodné vlastnosti a v některých případech se opravdu vyskytuje v přírodě a v různých odvětví matematiky, ovšem tyto mýty a dezinformace ji na kráse lehce ubírají.